


suivant: Correction de l'exercice
monter: Correction des exercices
précédent: Correction de l'exercice
Table des matières

On pose
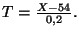
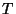 suit
suit
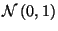 et
et
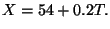
-
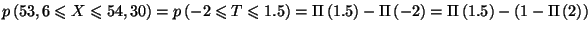 qui est donc la probabilité qu'une pièce soit bonne.
qui est donc la probabilité qu'une pièce soit bonne.
- La probabilité qu'une pièce soit défectueuse est donc
de
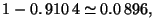 c'est à dire qu'il y a 8,9 % de pièces défectueuses.
c'est à dire qu'il y a 8,9 % de pièces défectueuses.
-
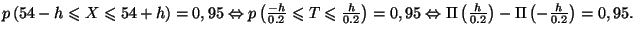 Ceci équivaut à
Ceci équivaut à
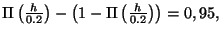 d'où
d'où
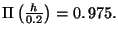 Par lecture inverse de la table de la loi normale centrée réduite,
on obtient
Par lecture inverse de la table de la loi normale centrée réduite,
on obtient
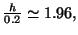 d'où
d'où
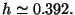 Les côtes d'alerte sont donc égales à
Les côtes d'alerte sont donc égales à 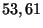 et
et 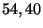 millimètres.
millimètres.
Michel
2002-07-27
![[*]](crossref.png)
![[*]](crossref.png)
![]()
![]()
![]() suit
suit
![]() et
et
![]()