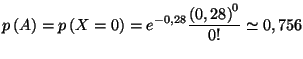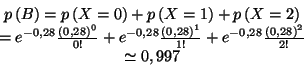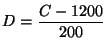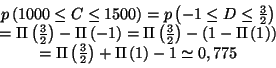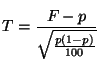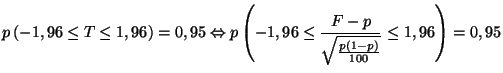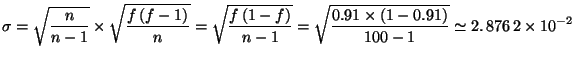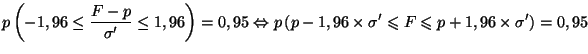


suivant: À propos de ce
monter: Correction des exercices
précédent: Correction de l'exercice
Table des matières
- On a :
- L'évènement B est l'union des évènements deux
à deux incompatibles '' un véhicule tiré au hasard
dans la parc a eu exactement 0 sinistre pendant l'année considérée
'', '' un véhicule tiré au hasard dans la parc a eu exactement
1 sinistre pendant l'année considérée '' et '' un
véhicule tiré au hasard dans la parc a eu exactement 2 sinistres
pendant l'année considérée ''. Donc
- Nous avons une suite de 15 épreuves de Bernouilli indépendantes.
Chaque épreuve n'a que deux issues possibles : soit l'évènement
E est réalisé avec une probabilité de 0,6, soit il
n'est pas réalisé avec une probabilité de 0,4. Ceci
prouve que la variable aléatoire
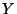 suit une loi binomiale
de paramètres 15 et 0,6.
suit une loi binomiale
de paramètres 15 et 0,6.
- On veut calculer la probabilité de l'évènement :
- Puisque
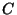 suit la loi normale de moyenne 1200 et d'écart type
200, la variable aléatoire
suit la loi normale de moyenne 1200 et d'écart type
200, la variable aléatoire 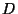 définie par
suit la loi normale centrée réduite. On trouve alors
ce qui permet facilement d'en déduire :
Il vient alors, en utilisant le formulaire :
définie par
suit la loi normale centrée réduite. On trouve alors
ce qui permet facilement d'en déduire :
Il vient alors, en utilisant le formulaire :
- L'estimation ponctuelle est donnée par le pourcentage obtenu
sur l'échantillon prélevé :
- On pose :
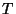 suit la loi normale centrée réduite. L'intervalle
de confiance pour
suit la loi normale centrée réduite. L'intervalle
de confiance pour 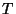 à 95% est défini par :
en utilisant le formulaire. On en déduit :
Afin de pouvoir obtenir un intervalle de confiance, il nous faut
dans ce cas approximer l'écart-type
à 95% est défini par :
en utilisant le formulaire. On en déduit :
Afin de pouvoir obtenir un intervalle de confiance, il nous faut
dans ce cas approximer l'écart-type
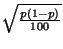 de
de 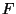 par
par 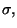 qui d'après le cours vaut
On en déduit ensuite :
On utilise l'estimation ponctuelle de
qui d'après le cours vaut
On en déduit ensuite :
On utilise l'estimation ponctuelle de 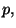 à savoir que
à savoir que
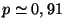 pour trouver que
pour trouver que
En conclusion, l'intervalle de confiance cherché est :
- Cette affirmation est fausse d'après le cours.



suivant: À propos de ce
monter: Correction des exercices
précédent: Correction de l'exercice
Table des matières
Michel
2002-07-27
![[*]](crossref.png)
![[*]](crossref.png)