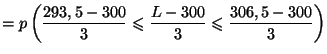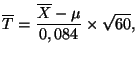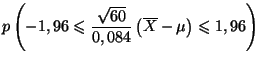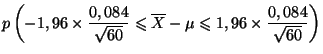


suivant: Correction de l'exercice
monter: Correction des exercices
précédent: Correction de l'exercice
Table des matières
- La variable
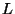 suit la loi normale
suit la loi normale
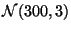 , donc la
variable
, donc la
variable 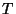 définie par
définie par
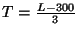 suit la loi normale
centrée réduite
suit la loi normale
centrée réduite
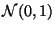 . Il vient alors
. Il vient alors
-
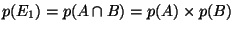 puisque
puisque 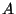 et
et 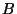 sont indépendants.
D'où
sont indépendants.
D'où
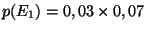 , soit
, soit
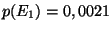 .
.
-
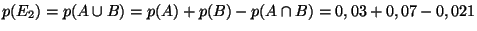 , soit
, soit
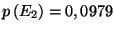 .
.
-
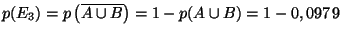 ,
soit
,
soit
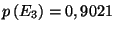 .
.
- On a 10 tirages indépendants, pour seulement 2 issues possibles
(
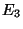 ou
ou
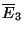 ), on est bien dans le cadre d'une
loi binômiale. Donc
), on est bien dans le cadre d'une
loi binômiale. Donc  suit la loi binomiale
suit la loi binomiale
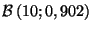 .
.
- Dans ce cas, on a
- La variable
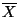 suit la loi normale
suit la loi normale
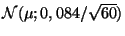 ,
et la moyenne sur un échantillon donné est
,
et la moyenne sur un échantillon donné est
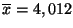 .
.
- L'estimation ponctuelle est
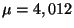 .
.
- On veut trouver le réel positif
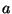 tel que
tel que
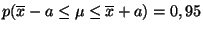 .
Introduisons la variable
.
Introduisons la variable
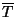 définie par
alors
définie par
alors
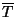 suit la loi normale centrée réduite
suit la loi normale centrée réduite
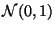 et l'on sait que pour tout réel positif
et l'on sait que pour tout réel positif 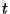 on a
Un coup d'
on a
Un coup d' il sur le formulaire nous montre qu'il faut choisir
il sur le formulaire nous montre qu'il faut choisir
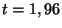 pour obtenir une probabilité de
pour obtenir une probabilité de 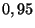 . Autrement
dit, on sait que l'on a
. Autrement
dit, on sait que l'on a
D'où ici l'intervalle de confiance à 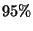 cherché
cherché
![$ I=\left[3,991;4,033\right]$](img409.gif) .
.
- Bien sûr, l'affirmation proposée est fausse : avec un intervalle
de confiance à
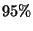 on est encore très loin d'une certitude.
on est encore très loin d'une certitude.



suivant: Correction de l'exercice
monter: Correction des exercices
précédent: Correction de l'exercice
Table des matières
Michel
2002-07-27
![[*]](crossref.png)
![[*]](crossref.png)