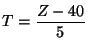


suivant: Correction de l'exercice
monter: Correction des exercices
précédent: Correction de l'exercice
Table des matières
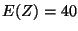 et
et 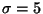 .
.
- On pose
Comme
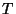 suit la loi normale centrée réduite, on en déduit que
suit la loi normale centrée réduite, on en déduit que
- Montrer d'abord que
puis que
ce qui permet de déterminer que
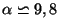 .
.
Michel
2002-07-27
![[*]](crossref.png)
![[*]](crossref.png)