



suivant: Fonctions usuelles
monter: Fonctions d'une variable réelle
précédent: Exercices
Table des matières
Solution 2.1 : a) 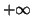 b)
b) 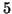 c)
c)
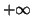 d)
d)
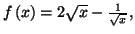 d'où
d'où
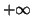
Solution 2.2 : a) 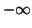 b)
b)
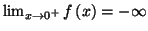 et
et
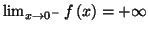 c)
c) 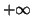 d)
d) 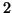
Solution 2.3 : b)
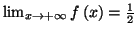 et
et
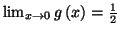
Solution 2.4 On a :
a)
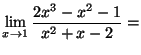
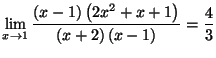
b)
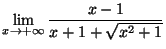 =
=
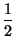 ( Factoriser par
( Factoriser par  au numérateur et au dé
nominateur)
au numérateur et au dé
nominateur)
c)
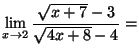
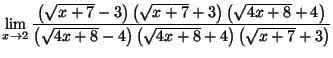
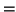
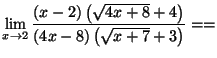
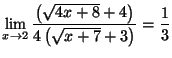
d)
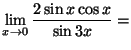
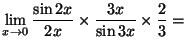
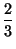
e)
 car
car

f)
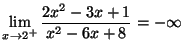 et
et
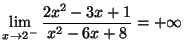
Solution 2.5 : a) 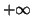 b)
b) 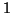 c)
c) 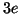 d) 0 e) +
d) 0 e) +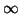 f) 0
f) 0
Solution 2.6 : Pour 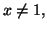 on a
on a
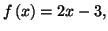 donc
donc
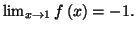 Cette
valeur étant distincte de
Cette
valeur étant distincte de
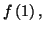 on peut affirmer que la
fonction
on peut affirmer que la
fonction  n'est pas continue en
n'est pas continue en 
Solution 2.7 : On a :
donc la fonction  est prolongeable par continuité en
est prolongeable par continuité en 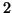 en une
fonction
en une
fonction 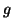 définie par :
On a aussi
définie par :
On a aussi
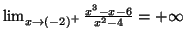 et
et
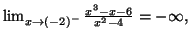 donc
donc  n'est pas
prolongeable par continuité en
n'est pas
prolongeable par continuité en
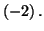
Solution 2.8 : On montre que la fonction
définit une bijection ( fonction continue strictement décroissante )
de
![$ \left[ 0,\pi\right]
$](img297.gif) dans
dans
![$ \left[ -\frac{\pi}{2},2\right] .$](img498.gif) Le
réel 0 admet donc un unique antécédent par cette fonction,
noté
Le
réel 0 admet donc un unique antécédent par cette fonction,
noté 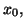 et ayant pour valeur approchée 1,714.
et ayant pour valeur approchée 1,714.
Solution 2.9 : (1) Aire du triangle AOB :
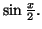
Aire hachurée :
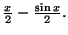 Les aires sont égales si et seulement si
Les aires sont égales si et seulement si
(2) La fonction  est croissante de
est croissante de
![$ \left[ 0,\frac{\pi}{3}\right] $](img503.gif) sur
sur
![$ \left[ 0,\frac{\sqrt{3}}{2}-\frac{\pi}{6}\right] ,$](img504.gif) et décroissante de
et décroissante de
![$ \left[ \frac{\pi}{3},\pi\right] $](img505.gif) sur
sur
![$ \left[ \frac{\sqrt{3}}{2}-\frac
{\pi}{6},-\frac{\pi}{2}\right] .$](img506.gif) On applique le théorème des
fonctions continues strictement monotones sur chacun des intervalles
précédents.
On applique le théorème des
fonctions continues strictement monotones sur chacun des intervalles
précédents.
(3) Par la méthode de dichotomie, on trouve
que
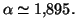
Solution 2.10 : On obtient les résultats
suivants :
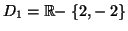 et
et
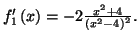
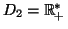 et
et
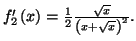
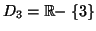 et
et

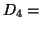
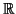 et
et
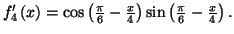
Solution 2.11 :
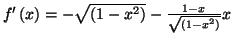 =
=

![$ \quad\forall x\in\left] -1,1\right[ .$](img518.gif)
On calcule
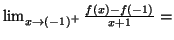
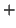
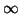 donc
donc  n'est pas dérivable en
n'est pas dérivable en
 , mais sa courbe représentative admet une demi-tangente verticale au
point d'abscisse
, mais sa courbe représentative admet une demi-tangente verticale au
point d'abscisse 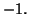
De même,
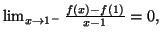 donc
donc  est dérivable en
est dérivable en 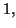 et
et
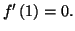 La courbe
représentative de
La courbe
représentative de  admet une demi-tangente horizontale au point
d'abscisse
admet une demi-tangente horizontale au point
d'abscisse 
Solution 2.12 : Comme
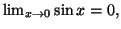 on peut identifier avec le développement limité à
l'ordre
on peut identifier avec le développement limité à
l'ordre 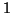 en 0 de la fonction
en 0 de la fonction  , ce qui permet d'obtenir
, ce qui permet d'obtenir

Solution 2.14 : On a
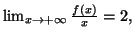 donc
donc 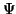 a pour direction
asymptotique la droite d'équation
a pour direction
asymptotique la droite d'équation 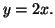
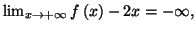 donc
donc 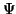 possède une branche
parabolique.
possède une branche
parabolique.
Solution 2.15 : On résout le système
d'équations obtenu à partir des conditions
 et
et
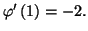 On trouve que
On trouve que 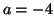 et
et 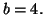
Solution 2.19 :
-
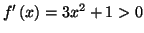 sur
sur
 donc
donc  est
strictement croissante sur
est
strictement croissante sur
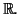
- On a
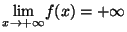 et
et
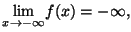 donc
donc  est une fonction
continue et strictement croissante de
est une fonction
continue et strictement croissante de
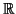 sur
sur
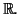 Le
théorème des valeurs intermédiaires permet d'affirmer qu'il existe
un unique
Le
théorème des valeurs intermédiaires permet d'affirmer qu'il existe
un unique 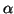 réel tel que
réel tel que
 Comme
Comme
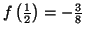 et
et
 on a
bien
on a
bien
 puisque
puisque
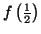 et
et
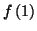 sont de signes contraires
sont de signes contraires Il suffit de remarquer que
comme
Il suffit de remarquer que
comme 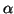 est solution de l'équation , la relation
est solution de l'équation , la relation
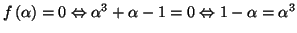
- Equation de la tangente à
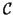 au point d'abscisse
au point d'abscisse  :
:
 Cette tangente coupe l'axe des
abscisses en un point
Cette tangente coupe l'axe des
abscisses en un point  d'abscisse
d'abscisse
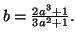
-
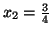 et
et 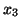 =
=
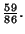
- On applique le résultat de la question 3) a) à
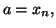 et on
a
et on
a
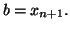
-
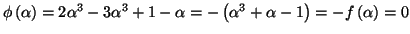
-
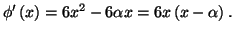 Or pour
Or pour
![$ x\in\left] \alpha,+\infty\right[ $](img557.gif)
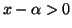 et
et
 donc
donc
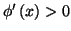 sur
sur
![$ \left]
\alpha,+\infty\right[ ,$](img561.gif) ce qui prouve bien que la fonction
ce qui prouve bien que la fonction 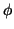 est
strictement croissante sur
est
strictement croissante sur
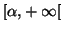 .
.
-
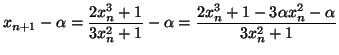 =
=
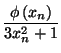
- On appelle
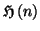 l'hypothèse de
récurrence à l'ordre
l'hypothèse de
récurrence à l'ordre 
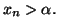
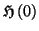 est vraie, puisque
est vraie, puisque

On suppose que
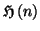 est vraie. On a donc
est vraie. On a donc
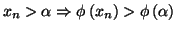 d'après la stricte
croissante de
d'après la stricte
croissante de 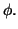 Comme
Comme
 et que
et que
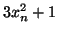
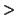 0, on a alors
donc
0, on a alors
donc
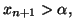 ce qui démontre que
ce qui démontre que
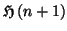 est bien vérifiée. Le principe du raisonnement par récurrence
permet de conclure que pour tout entier
est bien vérifiée. Le principe du raisonnement par récurrence
permet de conclure que pour tout entier 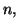
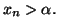
-
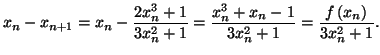 On
remarque alors que
On
remarque alors que  étant strictement croissante sur
étant strictement croissante sur

 Donc
Donc
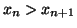 pour tout entier
naturel
pour tout entier
naturel 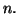
- La suite
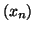 est décroissante et minorée
par
est décroissante et minorée
par 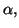 donc elle converge vers une limite
donc elle converge vers une limite  Comme pour tout
Comme pour tout 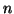 de
de

 le passage à la
limite et la continuité de la fonction
le passage à la
limite et la continuité de la fonction
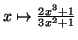 fournit l'égalité :
en utilisant l'unicité de la solution de l'équation
fournit l'égalité :
en utilisant l'unicité de la solution de l'équation
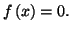
- On obtient les valeurs approchées suivantes :
Solution 2.20 :
1.
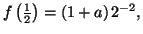 ce qui permet
d'obtenir
ce qui permet
d'obtenir  On posera donc pour toute la suite de l'exercice
On posera donc pour toute la suite de l'exercice

2.
![$ \sqrt[3]{f\left( 2\right) }=\sqrt[3]{2^{2}\times 2^{-\frac{1}{2}}}=\sqrt[%%
3]...
...{2}}}=\left( 2^{\frac{3}{2}}\right) ^{\frac{1}{3}}=2^{\frac{1}{%%
2}}=\sqrt{2}.$](img590.gif)
3.
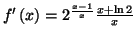 car
car
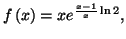 ce qui permet d'en déduire que :
ce qui permet d'en déduire que :
4. Comme
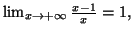 on en déduit que
on en déduit que
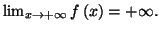 Ce résultat est évidemment le même quand
Ce résultat est évidemment le même quand  tend vers
tend vers 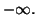
5.
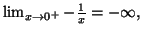 donc
donc
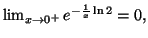 ce qui prouve
que
ce qui prouve
que

6. Posons
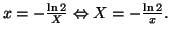 Si
Si  tend vers 0 par valeurs inférieures, alors
tend vers 0 par valeurs inférieures, alors 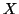 tend vers
tend vers 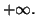 On a donc l'égalité :
On a donc l'égalité :
en utilisant la limite de cours
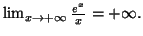
7. D'après la question 3, le signe de
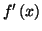 est
le signe de
est
le signe de
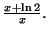 On en déduit donc le sens de variation
de
On en déduit donc le sens de variation
de  puis son tableau de variations, puis sa courbe :
puis son tableau de variations, puis sa courbe :
9.
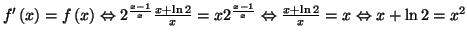 sur le domaine de définition
de
sur le domaine de définition
de  Par résolution de cette équation du second degré, on
trouve que l'équation admet deux solutions qui sont :
Par résolution de cette équation du second degré, on
trouve que l'équation admet deux solutions qui sont :
 et
et
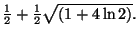
La fonction  n'est pas solution de l'équation différentielle
n'est pas solution de l'équation différentielle
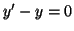 , car la relation
, car la relation
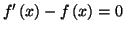 n'est pas vérifiée pour tout
n'est pas vérifiée pour tout  de
de




suivant: Fonctions usuelles
monter: Fonctions d'une variable réelle
précédent: Exercices
Table des matières
Michel
2002-08-06
![]() b)
b) ![]() c)
c)
![]() d)
d)
![]() d'où
d'où
![]()
![]() b)
b)
![]() et
et
![]() c)
c) ![]() d)
d) ![]()
![]() et
et
![]()
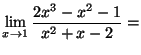
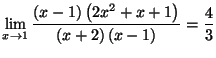
![]() =
=
![]() ( Factoriser par
( Factoriser par ![]() au numérateur et au dé
nominateur)
au numérateur et au dé
nominateur)
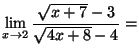
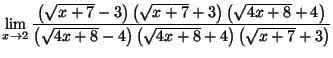
![]()
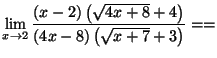
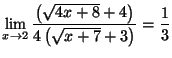
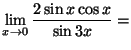
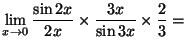
![]()
![]() car
car
![]()
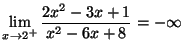 et
et
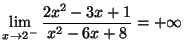
![]() b)
b) ![]() c)
c) ![]() d) 0 e) +
d) 0 e) +![]() f) 0
f) 0
![]() on a
on a
![]() donc
donc
![]() Cette
valeur étant distincte de
Cette
valeur étant distincte de
![]() on peut affirmer que la
fonction
on peut affirmer que la
fonction ![]() n'est pas continue en
n'est pas continue en ![]()
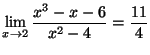
![\begin{displaymath}
\left\{
\begin{array}[c]{c}
g\left( x\right) =f\left( x\righ...
...\right\} \\
g\left( 2\right) =\frac{11}{4}
\end{array}\right.
\end{displaymath}](img493.gif)
![]()
![]() Les aires sont égales si et seulement si
Les aires sont égales si et seulement si
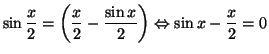
![]() et
et
![]()
![]() et
et
![]()
![]() et
et
![]()
![]()
![]() et
et
![]()
![]() =
=
![]()
![]()
![\includegraphics[
height=2.9014in,
width=3.1756in
]{fig1.ps}](img519.gif)
![]() on peut identifier avec le développement limité à
l'ordre
on peut identifier avec le développement limité à
l'ordre ![]() en 0 de la fonction
en 0 de la fonction ![]() , ce qui permet d'obtenir
, ce qui permet d'obtenir
![]()
![]() donc
donc ![]() a pour direction
asymptotique la droite d'équation
a pour direction
asymptotique la droite d'équation ![]()
![]() donc
donc ![]() possède une branche
parabolique.
possède une branche
parabolique.
![\includegraphics[
height=2.5996in,
width=3.064in
]{capes19.eps}](img531.gif)
![]() et
et
![]() On trouve que
On trouve que ![]() et
et ![]()
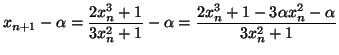 =
=
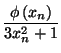
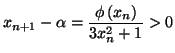
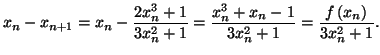 On
remarque alors que
On
remarque alors que 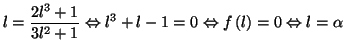
![$\displaystyle \begin{tabular}[c]{lll}
$x_{2}=\frac{3}{4}$\ & $x_{3}=\frac{59}{8...
...reak & $x_{9}=.\,68232\,78038\,28$\ &
$x_{10}=.\,68232\,78038\,28$\end{tabular}$](img586.gif)
![]() ce qui permet
d'obtenir
ce qui permet
d'obtenir ![]() On posera donc pour toute la suite de l'exercice
On posera donc pour toute la suite de l'exercice
![]()
![$ \sqrt[3]{f\left( 2\right) }=\sqrt[3]{2^{2}\times 2^{-\frac{1}{2}}}=\sqrt[%%
3]...
...{2}}}=\left( 2^{\frac{3}{2}}\right) ^{\frac{1}{3}}=2^{\frac{1}{%%
2}}=\sqrt{2}.$](img590.gif)
![]() car
car
![]() ce qui permet d'en déduire que :
ce qui permet d'en déduire que :
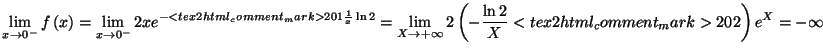
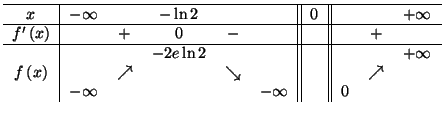
![]() sur le domaine de définition
de
sur le domaine de définition
de ![]() Par résolution de cette équation du second degré, on
trouve que l'équation admet deux solutions qui sont :
Par résolution de cette équation du second degré, on
trouve que l'équation admet deux solutions qui sont :
![]() et
et
![]()
![]() n'est pas solution de l'équation différentielle
n'est pas solution de l'équation différentielle
![]() , car la relation
, car la relation
![]() n'est pas vérifiée pour tout
n'est pas vérifiée pour tout ![]() de
de
![]()