



suivant: Equations différentielles
monter: Séries numériques
précédent: Exercices
Table des matières
Solution 7.1 : On calcule :
Comme
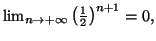 on en
déduit que la série
on en
déduit que la série
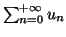 est convergente, et
que
est convergente, et
que
Solution 7.2 : Par le même raisonnement, on
montre que la série
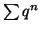 est convergente si et seulement si
est convergente si et seulement si
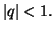 Dans ce cas, la série converge vers
Dans ce cas, la série converge vers
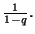
Solution 7.3 : On a la décomposition :
On peut donc calculer la somme partielle de la série :
On en déduit que la série est convergente, car
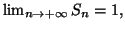 donc
donc
Solution 7.4 : On a la décomposition :
On peut donc calculer la somme partielle de la série :
On en déduit que la série est divergente, car
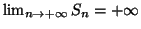 .
.
Solution 7.5 : On obtient :
avec 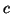 appartenant à l'intervalle d'extrémités 0 et
appartenant à l'intervalle d'extrémités 0 et 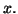 Prenons
Prenons 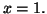 On en déduit donc que la somme partielle de la série
est donnée par :
De manière évidente, cette suite admet une limite en
On en déduit donc que la somme partielle de la série
est donnée par :
De manière évidente, cette suite admet une limite en  qui
vaut
qui
vaut 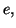 d'où l'égalité :
d'où l'égalité :
Solution 7.6 :
On a
La série de Riemann de terme général
 est
convergente, donc la série
est
convergente, donc la série
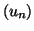 converge.
converge.
Pour 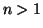 , on a
, on a
La série harmonique de terme général
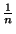 est divergente,
donc la série
est divergente,
donc la série
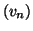 est divergente.
est divergente.
Solution 7.8 :
 est définie sur
est définie sur
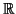 , paire et périodique, de période
, paire et périodique, de période
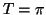 ; de plus
; de plus
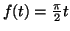 si
si
![$ t\in\left[0~,~\frac{\pi}{2}\right]$](img2110.gif) On obtient la courbe :
On obtient la courbe :
- Calculons les coefficients de Fourier
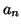 et
et 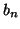 de la
fonction
de la
fonction  ; on a
; on a 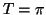 ,
,
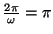 donc
donc
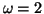 .
.
-
 est périodique de période
est périodique de période 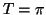 ; de plus :
; de plus :
- Comme
 est continue en tout point de
est continue en tout point de
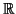 , la
série de Fourier de
, la
série de Fourier de  ,
,
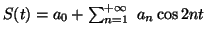 converge vers
converge vers 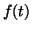 pour tout
pour tout  réel.
réel.
Or, sur
![$ [0~,~\frac{\pi}{2}]~~~~f(t)=\frac{\pi}{2}t$](img2144.gif) et sur
et sur
![$ [\frac{\pi}{2}~,~\pi]~~~~
f(t)=-\frac{\pi}{2}t+\frac{{\pi}^2}{2}$](img2145.gif)
Donc, sur
![$ [0~,~\frac{\pi}{2}]~~~~S(t)=\frac{\pi}{2}t$](img2146.gif) et sur
et sur
![$ [\frac{\pi}{2}~,~\pi]~~~~
S(t)=-\frac{\pi}{2}t+\frac{{\pi}^2}{2}$](img2147.gif)
-
-
D'après ce qui précède, en
 on aura
on aura
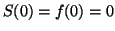 et donc :
et donc :
- Calculons le carré de la valeur efficace de
 :
car
:
car  étant paire,
étant paire, 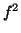 l'est aussi.
l'est aussi.
Avec la formule de Parseval
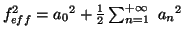
on obtient :
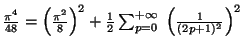
d'où
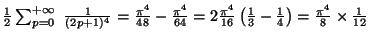
d'où
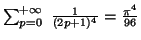
Solution 7.9 :
- Calculons la première intégrale :
et la seconde intégrale :
-
- La représentation graphique à l'allure suivante :
De plus 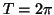 donc
donc
 .
.
- Calculons
 :
:
Calculons 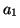 :
:
Calculons 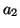 :
:
On admet que
 et
et 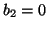 .
.
-
- Calculons
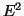 si
si 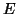 est la valeur efficace de
est la valeur efficace de 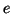 :
:
- D'après la formule de Bessel-Parseval on a :
Calculons
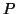 :
:
donc
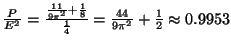 donc la valeur
approchée cherchée est
donc la valeur
approchée cherchée est 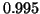 .
.
Solution 7.10 :
On a affaire à une série de terme positif. Utilisons le critère de
d'Alembert :
ce qui prouve que la série est convergente.
Solution 7.11 :
Justifier la minoration suivante, valable pour tout 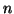 non-nul :
non-nul :
Or, la série de terme général
est divergente car son terme général équivaut à
qui est la terme général d'une série divergente. On en conclut par
les règles de comparaison que la série étudiée est divergente.
Solution 7.12 :
En utilisant le changement de variable proposé, on a :
Comme les séries
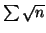 et
et
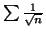 sont
divergentes, il faut donc que
Dans ce cas, on a alors :
qui est une série convergente ( voir les séries de Riemann ).
sont
divergentes, il faut donc que
Dans ce cas, on a alors :
qui est une série convergente ( voir les séries de Riemann ).




suivant: Equations différentielles
monter: Séries numériques
précédent: Exercices
Table des matières
Michel
2002-08-06
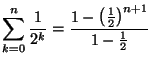
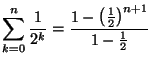
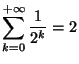
![]() est convergente si et seulement si
est convergente si et seulement si
![]() Dans ce cas, la série converge vers
Dans ce cas, la série converge vers
![]()
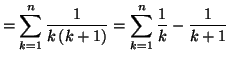
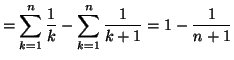

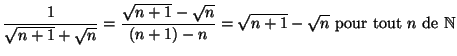
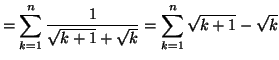
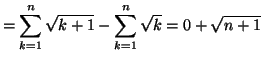
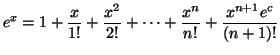
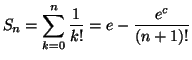
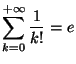
![]() , on a
, on a
![\includegraphics[scale=0.8]{capes21.eps}](img2111.gif)
![$\displaystyle a_0=\frac{1}{\pi}
\int_{ -\frac{\pi}{2} } ^{ \frac{\pi}{2} }
~f(t...
...{\pi}{2} \left[ \frac{t^2}{2} \right]
^{ \frac{\pi}{2} }_{0}
=\frac{{\pi}^2}{8}$](img2116.gif)
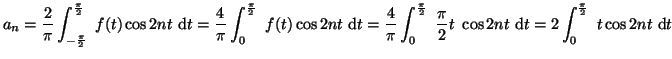
![$\displaystyle a_n=2\left[
\left[ \frac{t\sin 2nt}{2n} \right]_{0}^{ \frac{\pi}{2}}
-
\int_{0}^{ \frac{\pi}{2}} \frac{\sin 2nt}{2n}~{\rm d}t
\right]$](img2123.gif)
![$\displaystyle a_n=2\left[
0 -\frac{1}{2n} \left[ -\frac{\cos 2nt}{2n}
\right]_{...
...\pi}{2}}
\right]
= \frac{1}{2n^2}
\left( \cos \frac{2n\pi}{2} - \cos 0 \right)
$](img2125.gif)

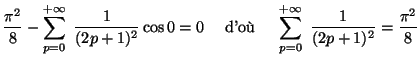
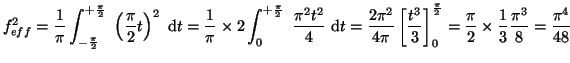
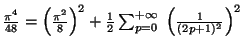
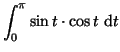
![$\displaystyle \int_0^{\pi} \frac{1}{2}\sin 2t ~{\rm d}t
=\frac{1}{2}\left[-\frac{1}{2}\cos 2t \right]_0^{\pi}$](img2159.gif)
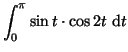

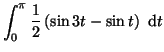
![$\displaystyle \frac{1}{2}\left[-\frac{1}{3}\cos 3t +\cos t \right]_0^{\pi}$](img2164.gif)
![$\displaystyle \frac{1}{2}\left[
\left( -\frac{1}{3}\cos 3\pi +\cos \pi \right)
-
\left( -\frac{1}{3}\cos 0 +\cos 0 \right)
\right]$](img2165.gif)
![$\displaystyle \frac{1}{2}\left[
\left( \frac{1}{3} -1 \right)
-
\left( -\frac{1}{3}+1 \right)
\right]$](img2166.gif)

![\includegraphics[scale=0.75]{capes22.eps}](img2168.gif)
![]() donc
donc
![]() .
.
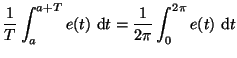
![$\displaystyle \frac{1}{2\pi}\int_0^{\pi} \sin t ~{\rm d}t
~~~~~ \textnormal{puisque}~~~~ e(t)=0
~~~~~ \textnormal{si}~~~~ t\in [\pi~,~2\pi]$](img2172.gif)
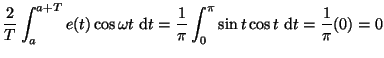
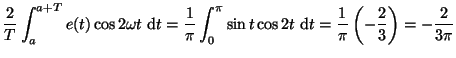
![$\displaystyle \frac{1}{T}\int_a^{a+T}\left[ e(t) \right]^2 ~{\rm d}t
=\frac{1}{...
...\rm d}t
~~~~\textnormal{car}~~~~e(t)=0
~~~~\textnormal{si}~~~~t\in [\pi~,~2\pi]$](img2179.gif)
![$\displaystyle \frac{1}{2\pi}\int_0^{\pi}
\frac{1}{2}\left( 1-\cos 2t \right)\ ~{\rm d}t
=\frac{1}{4\pi}\left[ t-\frac{1}{2}\sin 2t
\right]_0^{\pi}$](img2180.gif)
![$\displaystyle \frac{1}{4\pi}
\left[
\left( \pi-\frac{1}{2}\sin 2\pi \right)-0
\right]=\frac{1}{4}$](img2181.gif)
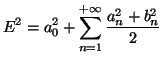
![$\displaystyle \left(\frac{1}{\pi} \right)^2+\frac{1}{2}
\left[ 0^2+
\left(\frac{1}{2} \right)^2+
\left(-\frac{2}{3\pi}
\right)^2+0^2
\right]$](img2184.gif)
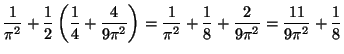
![]() non-nul :
non-nul :
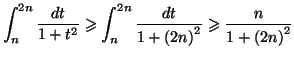
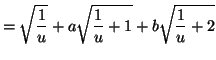
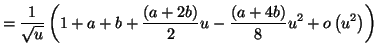
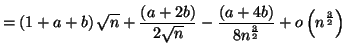
![\begin{displaymath}
\left\{
\begin{array}[c]{l}
1+a+b=0\\
a+2b=0
\end{array}\ri...
...rrow\left\{
\begin{array}[c]{l}
a=-2\\
b=1
\end{array}\right.
\end{displaymath}](img2199.gif)