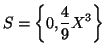Solution 1.1 : Les domaines de définition
sont égaux à
![]() Après simplification, il vient
:
Après simplification, il vient
:
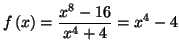 et
et
Solution 1.2 : Par identification des
coefficients, on trouve que ![]()
![]() et
et ![]()
Solution 1.3 : On trouve facilement
![]()
![]()
![]()
Solution 1.4 : On développe le polynôme
donné :
Solution 1.5 : On a
![]() et
et
![]() d'où
d'où ![]() et
et ![]()
Solution 1.6 : Pour tout ![]() de
de
![]()
![]() donc les racines éventuelles appartiennent
à
donc les racines éventuelles appartiennent
à
![]()
Solution 1.7 :
![]() Comme ces deux racines sont distinctes, on
en déduit que
Comme ces deux racines sont distinctes, on
en déduit que
![]() se factorise par
se factorise par
![]()
Solution 1.8 :
![]() entraîne que la somme des coefficients est nulle. Seul le polynôme du
cas a) est factorisable par
entraîne que la somme des coefficients est nulle. Seul le polynôme du
cas a) est factorisable par
![]() et on a :
et on a :
Solution 1.9 : On vérifie que
![]() et que
et que
![]() En effet :
En effet :
Solution 1.10 : On obtient :
Solution 1.11 : On remarque que :
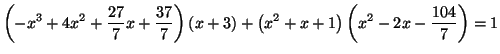
Solution 1.12 : On obtient :
| PGCD |
||
| PPCM |
Solution 1.14 : On obtient les résultats
suivants :
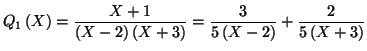
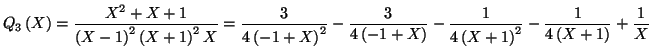
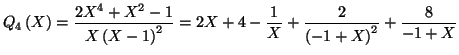
Solution 1.15 : On trouve :
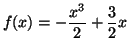
Solution 1.16 : Le polynôme d'interpolation de
Lagrange est défini par :
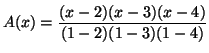
Solution 1.18 : On étudie sur
![]() la
fonction
la
fonction
Solution 1.19 : On appelle ![]() le degré de
le degré de ![]() . Vérifier que l'égalité proposée impose que
. Vérifier que l'égalité proposée impose que ![]() . A l'aide d'un système
d'équations, résoudre alors le problème posé. On démontrera que l'ensemble
. A l'aide d'un système
d'équations, résoudre alors le problème posé. On démontrera que l'ensemble ![]() des solutions est égal à :
des solutions est égal à :