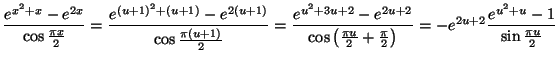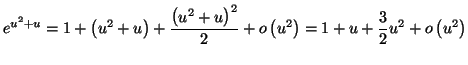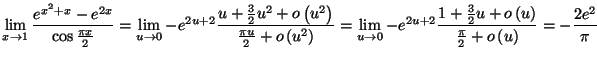Solutions des exercices

Solution 4.1 : Comme $\lim_{x\rightarrow 0}f\left( x\right) =1,$ on peut prolonger la fonction $f$ par continuité en posant $f\left( 0\right) =1.$ On fera l'abus de noter encore $f$ la fonction ainsi prolongée. On a de plus :

$$f^{\prime}\left( x\right) =\frac{\sin x-x\cos x}{\sin^{2}x}$$

En utilisant les égalités fournies, on trouve facilement que $\lim_{x\rightarrow0}f^{\prime}\left( x\right) =0,$ ce qui prouve que la fonction $f$ est dérivable en $0,$ et que $f^{\prime}\left( 0\right) =0.$

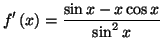
Solution 4.2 : Deux cas sont à examiner :
Si $x>1,$ la réponse est évidente.
Si $0\leqslant x\leqslant1,$ on applique l'égalité des accroissements finis à la fonction sinus entre $x$ et $0,$ et une majoration permet de conclure.

Solution 4.3 : 1) On applique l'égalité des accroissements finis à la fonction logarithme népérien sur $\left[ x,x+1\right] .$
2) Une sommation terme à terme permet d'obtenir l'encadrement valable pour tout $n\geqslant1$ :

$$\ln2-\frac{1}{2n}<S_{n}<\ln2$$

Le théorème des gendarmes permet de conclure facilement.

Solution 4.7 : On trouve en utilisant les règles de calcul sur les développements limités :

• $\frac{1}{1+x}=\allowbreak1-x+x^{2}-x^{3}+x^{4}-x^{5}+x^{6}+o\left( x^{6}\right) \allowbreak$

• $\frac{1}{1-x^{2}}=\allowbreak1+x^{2}+x^{4}+x^{6}+o\left( x^{6}\right)$

• $\frac{1}{1+x}+\frac{1}{1-x^{2}}=\allowbreak2-x+2x^{2}-x^{3} +2x^{4}-x^{5}+2x^{6}+o\left( x^{6}\right) \allowbreak\allowbreak$

Solution 4.9 : On effectue le produit des développements limités :

$$\ln\left( 1-x\right) =\allowbreak-x-\frac{1}{2}x^{2}-\frac{1}{3}x^{3} -\frac{1}{4}x^{4}+o\left( x^{4}\right)$$

$$\ln\left( 1+x\right) =\allowbreak x-\frac{1}{2}x^{2}+\frac{1}{3}x^{3} -\frac{1}{4}x^{4}+o\left( x^{4}\right)$$

En négligeant les termes d'ordre supérieur à $4,$ il vient :

$$\ln\left( 1-x\right) \ln\left( 1+x\right) =\allowbreak-x^{2}-\frac{5} {12}x^{4}+o\left( x^{4}\right)$$

Solution 4.12 : On applique la formule donnant le développement limité de $\left( 1+x\right) ^{-\frac{1}{2}}$ au voisinage de 0 et à l'ordre $2$ :

$$\frac{1}{\sqrt{1+x}}=\allowbreak1-\frac{1}{2}x+\frac{3}{8}x^{2}+o\left( x^{2}\right)$$

Par composition, il vient alors :

$$\frac{1}{\sqrt{1+x^{2}}}=\allowbreak1-\frac{1}{2}x^{2}+\frac{3}{8} x^{4}+o\left( x^{4}\right)$$

Solution 4.13 : On trouve successivement :

$$\sin x=\allowbreak x-\frac{1}{6}x^{3}+\frac{1}{120}x^{5}+o\left( x^{5}\right)$$

$$\ln\left( \frac{1+x}{1-x}\right) =\ln\left( 1+x\right) -\ln\left( 1-x\right) =\allowbreak2x+\frac{2}{3}x^{3}+o\left( x^{4}\right)$$

Par produit, en négligeant les termes d'ordre supérieur à $5,$ on a :

$$\left( \sin x\right) \ln\left( \frac{1+x}{1-x}\right) =\allowbreak 2x^{2}+\frac{1}{3}x^{4}+o\left( x^{5}\right)$$

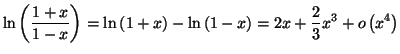
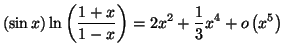
Solution 4.14 : On trouve :

$$\frac{x^{2}}{1+x}=\allowbreak x^{2}-x^{3}+x^{4}-x^{5}+x^{6}+o\left( x^{6}\right)$$

On pose $u=\frac{x^{2}}{1+x},$ qui tend bien vers 0 avec $x,$ et on utilise le développement limité de $\ln\left( 1+u\right)$ à l'ordre $3$ au voisinage de 0 :

$$\ln\left( 1+u\right) =\allowbreak u-\frac{1}{2}u^{2}+\frac{1}{3} u^{3}+o\left( u^{3}\right)$$

Ce qui permet d'obtenir :

$$\ln\left( 1+\frac{x^{2}}{1+x}\right) =\allowbreak x^{2}-x^{3}+x^{4} -x^{5}+x^{6}\allowbreak-\frac{1}{2... ...t( \allowbreak x^{2}-x^{3}+x^{4} -x^{5}+x^{6}+o\left( x^{6}\right) \right) ^{2}$$

$$+\frac{1}{3}\left( \allowbreak x^{2}-x^{3}+x^{4}-x^{5}+x^{6}+o\left( x^{6}\right) \right) ^{3}+o\left( x^{6}\right)$$

$$=\allowbreak x^{2}-x^{3}+\frac{1}{2}x^{4}-\frac{1}{6}x^{6}+o\left( x^{6}\right)$$

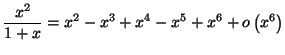
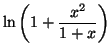Solution 4.15 : On effectue des dé veloppements limités à l'ordre 3 au voisinage de $0,$ ce qui fournit successivement :

$$\cos x=\allowbreak1-\frac{1}{2}x^{2}+o\left( x^{3}\right)$$

Par composition :

$$\ln\left( \cos x\right) =\allowbreak-\frac{1}{2}x^{2}+o\left( x^{3}\right)$$

Comme de plus $\left( 1-\cos2x\right) =\allowbreak2x^{2}+o\left( x^{3}\right) ,$ on obtient par division :

$$\frac{\ln\left( \cos x\right) }{1-\cos2x}=\allowbreak-\frac{1}{4}+o\left( 1\right)$$

ce qui permet d'obtenir $\lim_{x\rightarrow0}\,\frac{\ln\left( \cos x\right) }{1-\cos2x}=\allowbreak-\frac{1}{4}.$

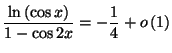
Solution 4.16 :
1) $f^{\prime}\left( x\right) =\allowbreak\frac{x^{2}-3}{\left( 1+x\right) \left( -1+x\right) }$ donc $f$ est croissante sur $\left] -1,1\right[ .$
2) $f\left( x\right) =\allowbreak1+3x+\frac{2}{3}x^{3}+o\left( x^{3}\right)$
3) L'équation de la tangente à la courbe représentative de $f$ au point d'abscisse 0 est $y=1+3x.$
4) On forme $f\left( x\right) -\left( 1+3x\right) ,$ et on montre que cette expression change de signe lorsque $x$ est de part et d'autre de $0,$ ce qui prouve bien que la courbe représentative de $f$ traverse sa tangente, donc que cette courbe admet un point d'inflexion d'abscisse 0.

Solution 4.17 : On trouve l'égalité :

$$x^{3}+x-5=\left( x^{2}-2x+1\right) \left( -5-9x-13x^{2}-16x^{3} -19x^{4}\right) -22x^{5}+19x^{6}$$

Solution 4.18 : On a successivement :
1) $1+\tan x=\allowbreak1+x+\frac{1}{3}x^{3}+o\left( x^{4}\right)$ et $1-\tan x=\allowbreak1-x-\frac{1}{3}x^{3}+o\left( x^{4}\right)$
2) Par division selon les puissances croissantes, on trouve :

$$\frac{1+\tan x}{1-\tan x}=\allowbreak1+2x+2x^{2}+\frac{8}{3}x^{3}+\frac{10} {3}x^{4}+o\left( x^{4}\right)$$

3) Il reste alors à effectuer une composition pour trouver

$$\ln\left( \frac{1+\tan x}{1-\tan x}\right) =\allowbreak2x+\frac{4}{3} x^{3}+o\left( x^{4}\right)$$

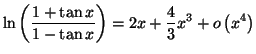
Solution 4.20 : On pose : $x=2+u.$ On a alors :

$$\sqrt{x}=\sqrt{2+u}=\sqrt{2}\sqrt{1+\frac{u}{2}}$$

Comme $u$ est dans un voisinage de $0,$ on peut utiliser le développement limité de $\sqrt{1+X}$ au voisinage de $0,$ d'où :

$$\sqrt{2+\frac{u}{2}}=\allowbreak\sqrt{2}+\left( \frac{\sqrt{2}}{8... ...}\right) u^{2}+\left( \frac{\sqrt{2}} {1024}\right) u^{3}+o\left( u^{3}\right)$$

Revenant à la variable initiale, on obtient :

$$\sqrt{x}=\allowbreak\sqrt{2}+\left( \frac{\sqrt{2}}{4}\right) \le... ...right) \allowbreak\left( x-2\right) ^{3}+o\left( \left( x-2\right) ^{3}\right)$$

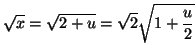
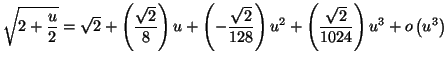
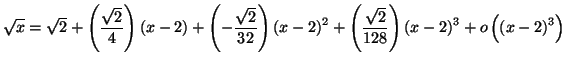
Solution 4.21 : On pose $x=u+\frac{\pi}{4}.$ On trouve :

$$\sqrt[3]{\tan x}=\allowbreak1+\frac{2}{3}\left( x-\frac{\pi}{4}\r... ...x-\frac{\pi}{4}\right) ^{2}+o\left( \left( x-\frac{\pi }{4}\right) ^{2}\right)$$

Solution 4.22 : On trouve facilement

$$f(x)=1-\frac{x}{2}+\frac{x^2}{6}+o(x^2)$$

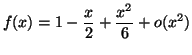
Solution 4.23 : Aisément :

$$\sqrt{1+x}-x=1-\frac{x}{2}-\frac{x^2}{8}+\frac{x^3}{16}+o(x^2)$$

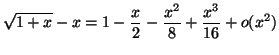
Solution 4.24 : Comme :

$$e^{2x}=1+2x+2x^2+\frac{4x^3}{3}+o(x^2)$$

il suffit de multiplier par $1-x$ pour obtenir le résultat cherché.

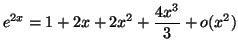
Solution 4.25 : On trouve :

$$f(x)-g(x)=\frac{x^3}{6}+o(x^3)$$

Au voisinage de 0, le signe de la différence est donc celui de $x^3$.

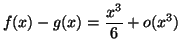
Solution 4.26 : Par les techniques usuelles, on trouve :

$$\frac{\sin\frac{x}{2}}{e^{2x}}=\frac{1}{2}x-x^{2}+\frac{47}{48}x^{3}+o\left( x^{3}\right)$$

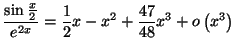
Solution 4.27 : Il vient à l'aide du changement de variable défini par $u=x+1$ :
$\ln\left( 2+x\right) =\allowbreak\left( x+1\right) -\frac{1}{2}\left( x+1\right) ^{2}+\frac{1}{3}\left( x+1\right) ^{3}+o\left( \left( x+1\right) ^{3}\right)$
$\sin\left( 1+x\right) =\allowbreak\left( x+1\right) -\frac{1}{6}\left( x+1\right) ^{3}+o\left( \left( x+1\right) ^{3}\right) ,$ d'où avec la technique de division selon les puissances croissantes :

$$\frac{\ln\left( 2+x\right) }{\sin\left( 1+x\right) }=1-\frac{1}{2... ... ^{2}-\frac{1}{12}\left( x+1\right) ^{3}+o\left( \left( x+1\right) ^{3}\right)$$

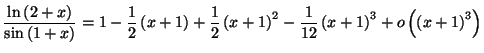
Solution 4.28 : Posons $x=u+1.$ On a :

$$\frac{e^{x^{2}+x}-e^{2x}}{\cos\frac{\pi x}{2}}=\frac{e^{\left( u+... ... {2}+\frac{\pi}{2}\right) }=-e^{2u+2}\frac{e^{u^{2}+u}-1}{\sin\frac{\pi u}{2}}$$

Comme $u$ est dans un voisinage de $0,$ on a

$$e^{u^{2}+u}=1+\left( u^{2}+u\right) +\frac{\left( u^{2}+u\right) ^{2}} {2}+o\left( u^{2}\right) =1+u+\frac{3}{2}u^{2}+o\left( u^{2}\right)$$

$$\sin\frac{\pi u}{2}=\frac{\pi u}{2}+o\left( u^{2}\right)$$

Après simplification, on obtient :

$$\lim_{x\rightarrow1}\frac{e^{x^{2}+x}-e^{2x}}{\cos\frac{\pi x}{2}... ...3}{2}u+o\left( u\right) }{\frac{\pi}{2}+o\left( u\right) }=-\frac{2e^{2}}{\pi}$$